◎律历一
○应天 乾元 仪天历
古者帝王之治天下，以律历为先。儒者之通天人，至律历而止。历以数始，
数自律生，故律历既正，寒暑以节，岁功以成，民事以序，庶绩以凝，万事根本，
由兹立焉。古人自入小学，知乐知数，已晓其原。后世老师宿儒犹或弗习律历，
而律历之家未必知道，各师其师，岐而二之。虽有巧思，岂能究造化之统会，以
识天人之蕴奥哉！是以审律造历，更易不常，卒无一定之说。治效之不古若，亦
此之由，而世岂察及是乎！
宋初承五代之季王朴制律历、作律准，以宣其声，太祖以雅乐声高，诏有司
考正。和岘等以影表铜臬暨羊头秬黍累尺制律，而度量权衡因以取正。然累代尺
度与望臬殊，黍有巨细，纵横容积，诸儒异议，卒无成说。至崇宁中，徽宗任蔡
京，信方士“声为律、身为度”之说，始大盭乎古矣。
显德《钦天历》亦朴所制也，宋初用之。建隆二年，以推验稍疏，诏王处讷
等别造新历。四年，历成，赐名《应天》，未几，气候渐差。太平兴国四年，行
《乾元历》，未几，气候又差。继作者曰《仪天》，曰《崇天》，曰《明天》，
曰《奉元》，曰《观天》，曰《纪元》，迨靖康丙午，百六十余年，而八改历。
南渡之后，曰《统元》，曰《乾道》，曰《淳熙》，曰《会元》，曰《统天》，
曰《开禧》，曰《会天》，曰《成天》，至德佑丙子，又百五十年，复八改历。
使其初而立法吻合天道，则千岁日至可坐而致，奚必数数更法，以求幸合玄象哉！
盖必有任其责者矣。
虽然，天步惟艰，古今通患，天运日行，左右既分，不能无忒。谓七十九年
差一度，虽视古差密，亦仅得其概耳。又况黄、赤道度有斜正、阔狭之殊，日月
运行有盈缩、朏朒、表里之异。测北极者，率以千里差三度有奇，晷景称是。
古今测验，止于岳台，而岳台岂必天地之中？余杭则东南，相距二千余里，华夏
幅员东西万里，发敛晷刻岂能尽谐？又造历者追求历元，逾越旷古，抑不知二帝
授时齐政之法，毕殚于是否乎？是亦儒者所当讨论之大者，诿曰星翁历生之责可
哉？至于仪象推测之具，虽亦数改，若熙宁沈括之议、宣和玑衡之制，其详密精
致有出于淳风、令瓒之表者，盖亦未始乏人也。今其遗法具在方册，惟《奉元》、
《会天》二法不存。旧史以《乾元》、《仪天》附《应天》，今亦以《乾道》、
《淳熙》、《会元》附《统元》，《开禧》、《成天》附《统天》。大抵数异术
同，因仍增损，以追合乾象，俱无以大相过，备载其法，俾来者有考焉。
昔黄帝作律吕，以调阴阳之声，以候天地之气。尧则钦若历象，以授人时，
以成岁功，用能综三才之道，极万物之情，以成其政化者也。至司马迁、班固叙
其指要，着之简策。自汉至隋，历代祖述，益加详悉。暨唐贞观迄周显德，五代
隆替，逾三百年，博达之士颇亦详缉废坠，而律志皆阙。宋初混一寓内，能士毕
举，国经王制，悉复古道。《汉志》有备数、和声、审度、嘉量、权衡之目，后
代因之，今亦用次序以志于篇。
曰备数。《周礼》，保氏教国子以六艺，其六曰九数，谓方田、粟米、差分、
少广、商功、均输、方程、赢朒、旁要，是为九章。其后又有《海岛》、《孙
子》、《五曹》、《张丘建》、《夏侯阳》、《周髀》、《缀术》、《缉古》等
法相因而起，历代传习，谓之小学。唐试右千牛卫胄曹参军陈从运着《得一算经》，
其术以因折而成，取损益之道，且变而通之，皆合于数。复有徐仁美者，作《增
成玄一法》，设九十三问，以立新术，大则测于天地，细则极于微妙，虽粗述其
事，亦适用于时。古者命官属于太史，汉、魏之世，皆在史官。隋氏始置算学博
士于国庠，唐增其员，宋因而不改。
曰和声。《周礼》，典同掌六律六同之和，凡为乐器，以十有二律为之数度。
古之圣人推律以制器，因器以宣声，和声以成音，比音而为乐。然则律吕之用，
其乐之本欤！以其相生损益，数极精微，非聪明博达，则罕能详究。故历代而下，
其法或存或阙，前史言之备矣。周显德中，王朴始依周法，以秬黍校正尺度，长
九寸，虚径三分，为黄钟之管，作律准以宣其声。宋乾德中，太祖以雅乐声高，
诏有司重加考正。时判太常寺和岘上言曰：“古圣设法，先立尺寸，作为律吕，
三分损益，上下相生，取合真音，谓之形器。但以尺寸长短非书可传，故累秬黍
求为准的，后代试之，或不符会。西京铜望臬可校古法，即今司天台影表铜臬下
石尺是也。及以朴所定尺比校，短于石尺四分，则声乐之高，盖由于此。况影表
测于天地，则管律可以准绳。”上乃令依古法，以造新尺并黄钟九寸之管，命工
人校其声，果下于朴所定管一律。又内出上党羊头山秬黍，累尺校律，亦相符合。
遂下尚书省集官详定，众议佥同。由是重造十二律管，自此雅音和畅。
曰审度者，本起于黄钟之律以秬黍中者度之，九十黍为黄钟之长，而分、寸、
尺、丈、引之制生焉。宋既平定四方，凡新邦悉颁度量于其境，其伪俗尺度逾于
法制者去之。乾德中，又禁民间造者。由是尺度之制尽复古焉。
曰嘉量。《周礼》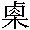，氏为量。《汉志》云，物有多少受以量，本起于黄钟
之管容秬黍千二百，而龠、合、升、斗、斛五量之法备矣。太祖受禅，诏有司精
考古式，作为嘉量，以颁天下。其后定西蜀，平岭南，复江表，泉、浙纳土，并、
汾归命，凡四方斗、斛不中式者皆去之。嘉量之器，悉复升平之制焉。
曰权衡之用，所以平物一民、知轻重也。权有五，曰铢、两、斤、钧、石，
前史言之详矣。建隆元年八月，诏有司按前代旧式作新权衡，以颁天下，禁私造
者。及平荆湖，即颁量、衡于其境。淳化三年三月三日，诏曰：“《书》云：
‘协时、月，正日，同律、度、量、衡。’所以建国经而立民极也。国家万邦咸
乂，九赋是均，顾出纳于有司，系权衡之定式。如闻秬黍之制，或差毫厘，锤钧
为奸，害及黎庶。宜令详定称法，着为通规。”事下有司，监内藏库、崇仪使刘
承珪言：“太府寺旧铜式自一钱至十斤，凡五十一，轻重无准。外府岁受黄金，
必自毫厘计之，式自钱始，则伤于重。”遂寻究本末，别制法物。至景德中，承
珪重加参定，而权衡之制益为精备，其法盖取《汉志》子谷秬黍为则，广十黍以
为寸，从其大乐之尺，（秬黍，黑黍也。乐尺，自黄钟之管而生也。谓以秬黍中
者为分寸、轻重之制。）就成二术，（二术谓以尺、黍而求氂、絫。）因度尺而
求氂，（度者，丈、尺之总名焉。因乐尺之源，起于黍而成于寸，析寸为分，析
分为氂，析氂为毫，析毫为丝，析丝为忽。十忽为丝，十丝为毫，十毫为氂，十
氂为分。）自积黍而取絫。（从积黍而取絫，则十黍为絫，十絫为铢，二十四铢
为两。锤皆以铜为之。）以氂、絫造一钱半及一两等二称，各悬三毫，以星准之。
等一钱半者，以取一称之法。其衡合乐尺一尺二寸，重一钱，锤重六分，盘重五
分。初毫星准半钱，至稍总一钱半，析成十五分，分列十氂；（第一毫下等半钱，
当五十氂，若十五斤称等五斤也。）中毫至稍一钱，析成十分，分列十氂；末毫
至稍半钱，析成五分，分列十氂。等一两者，亦为一称之则。其衡合乐分尺一尺
四寸，重一钱半，锤重六钱，盘重四钱。初毫至稍，布二十四铢，下别出一星，
等五絫；（每铢之下，复出一星，等五絫，则四十八星等二百四十絫，计二千四
百絫为十两。）中毫至稍五钱，布十二铢，列五星，星等二絫；（布十二铢为五
钱之数，则一铢等十絫，都等一百二十絫为半两。）末毫至稍六铢，铢列十星，
星等絫。（每星等一絫，都等六十絫为二钱半。）以御书真、草、行三体淳化钱，
较定实重二铢四絫为一钱者，以二千四百得十有五斤为一称之则。其法，初以积
黍为准，然后以分而推忽，为定数之端。故自忽、丝、毫、氂、黍、絫、铢各定
一钱之则。（谓皆定一钱之则，然后制取等称也。）忽万为分，（以一万忽为一
分之则，以十万忽定为一钱之则。忽者，吐丝为忽；分者，始微而着，言可分别
也。）丝则千，（一千丝为一分，以一万丝定为一钱之则。）毫则百，（一百毫
为一分，以一千毫定为一钱之则。毫者，毫毛也。自忽、丝、毫三者皆断骥尾为
之。）氂则十，（一十氂为一分，以一百氂定为一钱之则。氂者，氂牛尾毛也，
曳赤金成丝为之也。）转以十倍倍之，则为一钱。（转以十倍，谓自万忽至十万
忽之类定为则也。）黍以二千四百枚为一两，（一龠容千二百黍为十二铢，则以
二千四百黍定为一两之则。两者，以二龠为两。）絫以二百四十，（谓以二百
四十絫定为一两之则。）铢以二十四，（转相因成絫为铢，则以二百四十絫定成
二十四铢为一两之则。铢者，言殊异。）遂成其称。称合黍数，则一钱半者，计
三百六十黍之重。列为五分，则每分计二十四黍。又每分析为一十氂，则每氂计
二黍十分黍之四。（以十氂分二十四黍，则每氂先得二黍。都分成四十分，则一
絫又得四分，是每氂得二黍十分黍之四。）每四毫一丝六忽有差为一黍，则氂、
絫之数极矣。一两者，合二十四铢为二千四百黍之重。每百黍为铢，二百四十黍
为絫，二铢四絫为钱，二絫四黍为分。一絫二黍重五氂，六黍重二氂五毫，三黍
重一氂二毫五丝，则黍、絫之数成矣。其则，用铜而镂文，以识其轻重。新法既
成，诏以新式留禁中，取太府旧称四十、旧式六十，以新式校之，乃见旧式所谓
一斤而轻者有十，谓五斤而重者有一。式既若是，权衡可知矣。又比用大称如百
斤者，皆悬钧于架，植环于衡，环或偃，手或抑按，则轻重之际，殊为悬绝。至
是，更铸新式，悉由黍、絫而齐其斤、石，不可得而增损也。又令每用大称，必
悬以丝绳。既置其物，则却立以视，不可得而抑按。复铸铜式，以御书淳化三体
钱二千四百暨新式三十有三、铜牌二十授于太府。又置新式于内府、外府，复颁
于四方大都，凡十有一副。先是，守藏吏受天下岁贡金帛，而太府权衡旧式失准，
得因之为奸，故诸道主者坐逋负而破产者甚众。又守藏更代，校计争讼，动必数
载。至是，新制既定，奸弊无所指，中外以为便。（度、量、权、衡皆太府掌造，
以给内外官司及民间之用。凡遇改元，即差变法，各以年号印而识之。其印面有
方印、长印、八角印，明制度而防伪滥也。）
宋初，用周显德《钦天历》，建隆二年五月，以其历推验稍疏，乃诏司天少
监王处讷等别造历法。四年四月，新法成，赐号《应天历》。太平兴国间，有上
言《应天历》气候渐差，诏处讷等重加详定。六年，表上新历，诏付本监集官详
定。会冬官正吴昭素、徐莹、董昭吉等各献新历，处讷所上历遂不行。诏以昭素、
莹、昭吉所献新历，遣内臣沈元应集本监官属、学生参校测验，考其疏密。秋官
正史端等言：“昭吉历差。昭素、莹二历以建隆癸亥以来二十四年气朔验之，颇
为切准。复对验二历，唯昭素历气朔稍均，可以行用。”又诏卫尉少卿元象宗与
元应等，再集明历术吴昭素、刘内真、苗守信、徐莹、王熙元、董昭吉、魏序及
在监官属史端等精加详定。象宗等言：“昭素历法考验无差，可以施之永久。”
遂赐号为《乾元历》。《应天》、《乾元》二历皆御制序焉。
真宗嗣位，命判司天监史序等考验前法，研核旧文，取其枢要，编为新历。
至咸平四年三月，历成来上，赐号《仪天历》。凡天道运行，皆有常度，历象之
术，古今所同。盖变法以从天，随时而推数，故法有疏密，数有繁简，虽条例稍
殊，而纲目一也。今以三历参相考校，以《应天》为本，《乾元》、《仪天》附
而注之，法同者不复重出，法殊者备列于后。
建隆《应天历》
演纪上元木星甲子，距建隆三年壬戌，岁积四百八十二万五千五百五十八。
（《乾元》上元甲子距太平兴国六年辛巳，积三千五十四万三千九百七十七。《
仪天》自上元土星甲子至咸平四年辛丑，积七十一万六千四百九十七。）
步气朔
元法：一万二。（《乾元》元率九百四十。《仪天》宗法一万一百。又总谓
之日法。）
岁盈：二十六万九千三百六十五。（《乾元》岁周二十一万四千七百六十四。
《仪天》岁周三十六万八千八百九十七。《仪天》有周天三百六十五、余二千四
百七十，约余二千四百四十五；岁余五万二千九百七十、余二千四百七十。《应
天》、《乾元》无此法，后皆仿此。）
月率：五万九千七十三。（《乾元》不置此法。《仪天》合率二十九万八千
二百五十九。又《仪天》有岁闰一万九千八百六十二，月闰九千一百一十五、秒
六。）
会日：二十九、小余五千三百七。（《乾元》朔策二十九、小余一千五百六
十。《仪天》会日二十九、小余五千三百五十七。）
弦策：七、小余三千八百二十七、秒六。（《乾元》小余一千一百二十五。
《仪天》小余三千八百六十四、秒二十七。策并同。）
望策：十四、小余七千六百五十四、妙一十二。（《乾元》小余二千二百五
十七。《仪天》小余七千七百二十七、秒一十八。策并同。）
气策：十五、小余二千一百八十五、秒二十四。（《乾元》小余六百四十二
半。《仪天》小余二千二百七、秒三。策并同。又《仪天》有气盈四千四百一十
四、秒六。）
朔虚分：四千六百九十五。（《乾元》一千三百八十。《仪天》四千七百四
十一。）
没限：七千八百一十六、秒九。（《乾元》二千二百九十七半。《仪天》七
千八百九十二。又《仪天》有纪实六十万六千。）
秒法：二十四。（《乾元》一百。《仪天》秒母三十六。）
纪法：六十。（二历同。）
推元积：（《乾元》、《仪天》皆谓之求岁积分。）置所求年，以岁盈展之
为元积。
求天正所盈之日及分并冬至大小余：以八十四万一百六十八去元积，不尽者，
半而进位，以元法收为所盈日，不满为小余。日满六十去之，不满者，命从甲子，
算外，即冬至日辰、大小余也。（《乾元》以岁周乘积年为岁积分，以七万五百
六十去之，不尽，以五因，满元率收为日，不满为余日。《仪天》以岁周乘积年，
进一位，为岁积分；盈宗法而一为积日，不满为余日。去命并同《应天》。）
求次气：以天正冬至大、小余遍加诸常数，盈六十去之，不盈者，命如前，
即得诸气日辰、大小余秒也。（《乾元》置中气大、小余，以气策加之，命如前，
即次气日辰也。《仪天》置冬至大、小余，加气策及余秒，秒盈秒母从小余，盈
纪法去之，皆命如前法，各得次气常日辰及余秒。）
求天正十一月朔中日：（《乾元》谓之经朔。《仪天》谓之天正合朔。）以
月率去元积，不尽者，为天正十一月通余；以通余减七十三万六百三十五，余，
半而进位，以元法收为日，不满为分，即得所求天正十一月朔中日及余秒。
（《乾元》以一万七千三百六十四去岁积分，不尽为朔余；以岁积分为朔积分，
又倍五万二千九百二十，除之，余以五因，满元率为日，不满为分。《仪天》以
合率去岁积分，不尽为闰余；满宗法为闰日，不满为余，以闰日及余减天正冬至
大、小余，为天正合朔大、小余；去命如前，即得合朔日辰、大小余。）
求次朔望中日：（《乾元》谓之求弦望经朔。《仪天》谓之求次朔。）置朔
中日，累加弦策余秒，即得弦、望及次朔中日。（《乾元》以弦策加经朔大、小
余，即得次朔经日；以弦策及余秒加经朔，得上弦；再加，得望；三之，得下弦。）
求望中月：置朔中月，加半交，盈交正去之，余为望中月。（二历不立此法。）
求朔弦望入气：置朔、望中日，各以盈缩准去，不尽者，为入气日及分。
（二历不立此法。）
推没日：置有没之气小余，（其小余七千八百一十六、秒九以上者求之也。）
近减元法，余以八因之，一千九十二、秒一十九半除为没日，命起气初，即得没
日辰。其秒不足者，退一分，加二十四秒，然后除之，四分之三以上者进。（《
乾元》置有没之气小余，在二千二百九十七半以上者，以十五乘之，用减四万四
千七百四十二半，余以六百四十二半除为没日。《仪天》以秒母通常气小余及秒，
而从之以减岁周，余满五千二百九十七为没日，去命如前。）
推灭日：以冬至大、小余，遍加朔日中为上位，有分为下位，在四千六百九
十五以下者，为有灭之分也。置有灭之分，进位，以一千五百六十五除为灭日，
以灭日加上位，命从甲子，算外，即得月内灭日。（《乾元》置有灭之经朔小余，
在一千一百八十以下者，以八因之，满三百六十八除为灭日。《仪天》经朔小余
在朔虚法以下者，三因，进位，以朔虚分除为灭日。）
求发敛
候策：五、小余七百二十八、秒二，母二十四。（《乾元》候数五、小余一
百一十四、秒十二，秒母七十二。《仪天》候率五、小余七百三十五、秒二十五，
秒母三十六。）
卦策：六、小余八百七十四、秒六。（《乾元》卦位六、小余二百五十七，
秒母六十。《仪天》卦率六、小余八百八十三、秒二十。）
土王策：十二、小余一千七百四十八、秒一十二。（《乾元》策三、小余一
百二十八半，秒母一百一十。《仪天》土王率三、小余四百四十、秒五，秒母同
上。）
辰数：八百三十三半。（《乾元》辰法二百四十五，辰率千五百二十。）
刻法：一百。（《乾元》一百四十七。《仪天》刻三百。）
求七十二候：各因诸气大、小余秒命之，即初候日也；各以候策加之，得次
候日；又加之，得末候日。（二历同法。）
求六十四卦：各置诸中气大、小余秒命之，即公卦用事日；以卦策加之，得
次卦用事日；又加之，得终卦用事日。十有二节之初，皆诸侯外卦用事日。（二
历同法。）
求五行用事：各因四立大、小余秒命之，即春木、夏火、秋金、冬水首用事
日；以土王策加四季之节大、小余秒，命从甲子，算外。即其月土王用事日。
（《乾元》以土王策减四季中气大、小余。《仪天》以土王率加四季大、小余。）
求二十四气加时辰刻：（《乾元》谓之辰刻。《仪天》谓之求时。）各置小
余，以辰数除之为时数，不满，百收为刻分，命起子正，算外，即所在。（《乾
元》时数同，其不尽，以五因之，以刻法除为刻分。《仪天》以三因小余，以辰
率除之为时数，不尽者，满刻率除为刻，余为分。）
天总：七十三万六百五十八、秒六十四。（《乾元》轨率二十一万四千七十
七、秒七千五百一十、小分七十。《仪天》乾元数三百六十八万九千八十八、秒
九十九。）
天度：三百六十五、小余二千五百六十三、微八十八。（《乾元》周天三百
六十五度、小余二千五百六十三。《仪天》乾则三百六十五度、小余二千五百八
十八、秒九十九。《仪天》诸法皆在天总数中。《乾元》、《仪天》各立其法。
《乾元》周天策一百七万三千八百五十三、秒七千五百五十三半，会周一万七千
三百六十四，会余二十一万四千七百六十四，天中一百八十二、六千二百八十一
半。《仪天》岁差一百一十八、秒九十九，一象度九十一、余三千一百四十二、
秒五十，盈初缩末限分八十九万七千六百九十九、秒五十，限日八十八、余八千
八百九十九、秒五十，缩初盈末限分九十四万六千七百八十五、秒十五，限日九
十三、余七千四百八十五、秒五十，盈缩积二万四千五百四十三，进退率一千八
百三十六，秒母一百。）
《乾元》二十四气日躔阴阳度
（《应天》、《乾元》二历，以常气求其阴阳差，故有二十四气立成。《仪
天》以盈缩定分、四限直求二十四气阴阳差，乃更不制二十四气差法。）
求日躔损益盈缩度：（《乾元》谓之求每日阴阳差。《仪天》谓之求入盈缩
分先后定数。）各置定日及分，以冬至常数相减，百收，通为分，自雨水后十六
为法，自霜降后十五为法。除分为气中率，二相减，为合差；半之，加减率为初、
末率。（后多者，减为初、加为末；后少者，加为初、减为末。）又法，以除合
差，为日差。（后少者，日损初率；后多者，日益初率。）为每日日躔损益率；
累积其数，为盈缩度分。（《乾元》各置气数，以一百二十乘之，以一千八百二
十六除之，所得为平行率；相减，为合差；初、末并如《应天》。《仪天》以宗
法乘盈缩积，以其限分除之，为限率分，倍之，为未限平率；日分乘之，亦以限
分除之，为日差；半之，加减初、末限平率，在初者减初加末，在末者减末加初，
为末定率；乃以日差累加减限初定率，初限以减、末限以加，为每日盈缩定分；
各随其限盈加缩减其下先后数，为每日先后定数；冬至后积盈为先，在缩减之；
夏至后，积缩为后，在盈减之。其进退率、升平积准此求之，即各得其限每日进
退率、升平积也。）
求日躔先后定数：（《乾元》谓之求入气、求弦望气入、求日躔阴阳差。）
各以朔、弦、望入气日及减本气定日及分秒通之，下以损益率展，以元法为分，
损减益加次气下先后积为定数。（《乾元》以其月气节减经朔大、小余，即得入
气日及分；又以弦策累加天正朔日入气大、小余，满气策去之，即得弦、望经朔
入气日及分；以其日损益率乘入气日余分，所得，用损益其日阴阳差为定数。《
仪天》法见上。又《仪天》有求四正节定日，去冬、夏二至盈缩之中，先后皆空，
以常为定；其春、秋二分盈缩之极，以一百乘盈缩积，满宗法为日，先减后加，
去命如前，各得定日。若求朔、弦、望盈缩限日，以天正闰日及余减缩末限日及
分，余为天正十一月经朔加时入限日及余；以弦策累加之，即得弦、望及后朔初、
末限日；各置入限日及余，以其日进退率乘之，如宗法而一，所得，以进退其日
下升平积，即各为定数。）
赤道宿度
斗：二十六 牛：八 女：十二 虚：十（及分）
危：十七 室：十六 壁：九（二历同）
北方七宿九十八度。虚分二千五百六十三、秒一十九。（《乾元》七千五百
三十五、秒二十五。《仪天》二千五百八十八、秒九十九。）
奎：十六 娄：十二 胃：十四 昴：十一
毕：十七 觜：一 参：十
西方七宿八十一度。（二历同）
井：三十三 鬼：三 柳：十五 星：七
张：十八 翼：十八 轸：十七
南方七宿一百一十一度。（二历同）
角：十二 亢：九 氐：十五 房：五
心：五 尾：十八 箕：十一
东方七宿七十五度。（二历同）
（又《仪天》云：“前皆赤道度，自古以来，累依天仪测定，用为常准。赤
道者，天中纮带，仪极攸凭，以格黄道也。”）
求赤道变黄道度：（《乾元》谓之求黄道度。《仪天》谓之推黄道度。）准
二至赤道日躔宿次。前后五度为限，初限十二，每限减半，终九限减尽。距二立
之宿，减一度少强，又从尽起限，每限增半，九限终于十二。距二分之宿，皆乘
限度，身外除一，余满百为度分，命曰黄赤道差。二至前后各九限，以差为减；
二分前后各九限，以差为加。各加减赤道度为黄道度，有余分就近收为太、半、
少之数。（《乾元》初率九，每限减一，末率一。《仪天》初数一百七，每限减
一十，末率二十七，其余限数加减并同《应天》。）
黄道宿度
斗：二十三度半 牛：七度半（二历同） 女：十一度太（二历并十一
度半）虚：十度少强（二千五百六十三、秒十九。《乾元》无分。《仪天》六十
三分、九十九秒。危：十七度少（《乾元》同。《仪天》十七度太） 室：十六
度太。 壁：十度（《乾元》九度太。《仪天》同。）
北方七宿九十七度二千五百六十三、秒十九。（《乾元》九十六度半、《仪
天》九十七度半、六十三、秒九十九。）
奎：十七度半（二历同） 娄：一十二度太（《乾元》十三度。《仪天》同。）
胃：十四度少。（二历并十四度太） 昴：十一度（二历同） 毕：十六度
半（《乾元》同。《仪天》十六度少。） 觜：一度 参：九度少（二历并同）
西方七宿八十二度少。（《乾元》八十三度。《仪天》八十二度半。）
井：三十度 鬼：二度太（二历并同） 柳：十四度半（《乾元》、
《仪天》十四度少。）星：七度。（《乾元》、《仪天》并六度太。）
张：十八度少（《乾元》同。《仪天》十八度太。）翼：十九度少（《乾元》
十九度。《仪天》同）。
轸：十八度太（二历同）
南方七宿一百一十度半。（《乾元》一百九度太。《仪天》同。）
角：十三度 亢：九度半（二历并同） 氐：十二度少（《乾元》、
《仪天》并十五度半。） 房：五度（二历同） 心：五度（《乾元》同。《仪
天》四度太。） 尾：十七度少。（《乾元》同。《仪天》十七度。）
箕：十度（《乾元》十度太。《仪天》十度。）
东方七宿七十五度少。（《乾元》七十六度。《仪天》七十四度太。）
求赤道日度：（《仪天》谓之推日度。）以天总除元积，为总数；不尽，半
而进位，又以一百收总数从之，以元法收为度，不满为分秒，命起赤道虚宿四度
分。（《乾元》以轨率去岁积分，余以五因之，满轨率收为度，不满，退除为分，
余同。《仪天》以乾数去岁积分，宗法收为度，命起虚宿二度，余同《应天》。
又以一象度及余秒累加之，满赤道宿度即去之，各得四正，即初日加时赤道日度
也。）
求黄道日度：置冬至赤道日躔宿度，以所入限数乘之，所得，身外除一，满
百为度，不满为分，用减赤道日度，为冬至加时黄道日度及分。（《乾元》、
《仪天》亦如其法。《乾元》即以八十四，《仪天》以一百一除为度，余同《应
天》。）
求朔望常日月：（《乾元》谓之求黄道平朔日度。）置朔、望日躔先后定数，
进一位，倍之，身外除之，以元法收为度分，先加后减朔望中日、月，为朔望中
常日、月度分；用加冬至黄道之宿，命如前，即得朔望常日、月所在。（《乾元》
置会周一万七千三百六十，以距十一月后来月数乘之，所得，减去朔余，加会余
而半之，以二百九十四收为度，不尽，退除为分。《仪天》法在后。《乾元》又
有求黄道加时朔日度，置平朔日，以日躔阳加阴减之，又以冬至黄道日度加而命
之，即其朔加时黄道日度及分也。若求望日度者，以半朔策加之，即得望日度及
分也。用阳度，即依本术。）
每日加时黄道日度：（《乾元》谓之每日行分。）以定朔、望日所在相减，
余以距后日数除之，为平行分；二行分相减，为合差；半之，加减平行分，为初
行分；（后平行多，减为初；后平行少，加为初。）以距后日数除合差，为日差；
后少者损，后多者益，为每日行分；累加朔、望日，即得所求。（《乾元》同。
《仪天》不立此法。又《仪天》有求次正定日加时黄道日度，置岁差，以限数乘
之，退一位，满一百一为差秒及小分，再析之，乃以加一象度，所得，累加冬至
黄道日，满黄道宿次去之，各得四正，即加时黄道日度也。若求四正定日夜半黄
道日度，置其定日小余副之，以其日盈、缩分乘之，满宗法而一，盈加缩减其副，
乃以减其日加时，即为夜半黄道日度。又有求每日夜半日度，因四正初日夜半度，
累加一策，以其日盈缩分盈加缩减，满黄道宿次去之，即得每日夜半日度。又有
求定朔、弦、望加时日度，置定朔、望小余副之，以其日盈缩分乘之，以宗法收
之为分，盈加缩减其副，以加其日夜半度，各得其时加日躔所次。如朔、望有
进退者，此术不用。）